Es ist eines der großen Themen im Lauf der Schullaufbahn: Das Lösen quadratischer Gleichungen! Verschiedene Varianten werden in der Schule erarbeitet; die größten Schwierigkeiten bereitet jedoch im Allgemeinen das algebraische Lösen quadratischer Gleichungen – darum soll es hier gehen.
Wir tasten uns langsam an die Sache ran und erhöhen die Schwierigkeit dann schrittweise.
Inhaltsverzeichnis
x² = 9 – die einfachste quadratische Gleichung
Wir suchen eine Zahl, deren Quadrat 9 ergibt. Da muss man nicht groß überlegen: Die Lösung ist 3, denn 3 mal 3 ist 9. Falsch! Es gibt mehr als eine Lösung, denn auch $(-3)\cdot(-3)=9$. Richtig ist also: Die Lösungen sind 3 und -3.
Das ist einer der klassichen Schülerfehler und wird sich auch bei komplizierteren Gleichungen so fortziehen.
Wir gehen einen winzigen Schritt weiter. Denn schon die Gleichung \[x^2=2\] ist nicht mehr so einfach. Bis zu diesem Tag ist man im Unterricht meist der Ansicht, dass es keine solche Zahl gibt, deren Quadrat 2 ergibt. Richtig soweit. Da ist die Mathematik pragmatisch: Wir erfinden eine solche Zahl, die diese Eigenschaft hat: die Wurzel ist geboren. Die Wurzel aus 2, geschrieben $\sqrt{2}$, ist die positive Zahl, die im Quadrat 2 ergibt.
Folglich ist also $\sqrt{9}=3$. Achtung: Falsch ist hingegen $\sqrt{9}=-3$. Zwar hat die Gleichung $x^2=9$ die zwei Lösungen 3 und -3, als Wurzel wird jedoch die positive Zahl genommen. Schlichter Grund: Was ist $\sqrt{9}+\sqrt{9}$. wenn die Wurzel entweder plus oder minus 3 ist? Man wollte Eindeutigkeit, also ist $\sqrt{9}+\sqrt{9}=3+3=6$
x²+6x=0 – Ausklammern hilft
Es gibt diesen Satz, den Schülern und Lehrern bei diesem Thema zu den Ohren herauskommt: Ein Produkt ist immer dann gleich null, wenn einer der Faktoren null ist.
Helfen tut der Satz aber erst, wenn auch tatsächlich ein Produkt vorkommt. Das erreichen wir, indem wir ausklammern:
\begin{align*} x^2+6x&=0 \\ x\cdot(x+6)&=0 \end{align*}
Die Faktoren sind hier also $x$ und $(x+6)$. Das Produkt ist also null, wenn
\begin{align*}x&=0 && \text{ oder } & (x+6) &=0 \\x&=0 && \text{ oder } & x &=-6 \\\end{align*}
Die Gleichung hat also die Lösungen $x=0$ oder $x=-6$.
x²+6x+9=0 – Arbeit mit der binomischen Formel
Ein wichtiger Zwischenschritt auf dem Weg zur Quadratischen Ergänzung liefert uns ein Blick auf diese Gleichung. Links des Gleichzeichens muss einem etwas auffallen; uns helfen die Binomische Formeln! Wir können die Gleichung massiv vereinfachen, wenn wir erkennen, dass wir links die binomische Formel anwenden können. Es ist nämlich \[x^2+6x+9=(x+3)^2\] Das hilft uns, denn danach können wir fast genauso vorgehen wie im ersten Fall und die Wurzel ziehen:
\begin{align*}x^2+6x+9&=0\\ (x+3)^2&=0 \\ x+3&= 0 \\ x&=-3\end{align*}
Diese quadratische Gleichung hat also tatsächlich nur eine Lösung, nämlich x=-3.
x²+6x+8=0 – Quadratische Ergänzung
Nun, diese Gleichung ist doch fast genauso wie vorher. Es muss also eine Möglichkeit geben, auch diese Gleichung zu lösen. Was stört, ist, dass links vom Gleichheitszeichen diesmal keine binomische Formel zu entdecken ist.
Zentrale Idee der Quadratischen Ergänzung: Wenn da keine binomische Formel zu erkennen ist, dann tricksen wir uns da eben eine hin!
Wie wir im Beispiel vorher erkannt haben, würde es uns helfen, wenn dort $x^2+6x+9$ stehen würde. Wir können nicht einfach aus der 8 eine 9 machen, das würde die Gleichung verändern.
Der Clou: Wir ergänzen in der Gleichung $+9-9$. Das wirkt auf dem ersten Blick erstmal unsinnig, ermöglicht uns jedoch eine starke Vereinfachung mit Hilfe der binomischen Formel.
\begin{align*}x^2+6x+8&= 0 & \color{orange}{\text{Quadratische Ergänzung}} \\\underbrace{x^2+6\color{orange}{+9}}_{(x+3)^2}\color{orange}{-9}+8&=0 &\text{Binomische Formel} \\(x+3)^2-9+8&=0 & \text{Zusammenfassen} \\(x+3)^2-1&=0 & \big|+ 1 \\(x+3)^2 &=1 & \text{Wurzel ziehen} \\x+3 &= \pm 1 & \big|-3 \\x=-2 \text{ oder } x&=-4\end{align*}
Die Lösungen der Gleichungen sind also $x=-2$ oder $x=-4$.
x²+6x+10=0 – Quadratische Ergänzung ohne Lösung
Wiederum ist diese Gleichung sehr ähnlich zu denen, die wir schon gelöst haben. Trotzdem liefert uns diese Gleichung eine neue Erkenntnis: Nicht alle quadratischen Gleichungen haben eine Lösung. Wir werfen einen kurzen Blick auf den Funktionsgraphen von $f(x)=x^2+6x+10$:
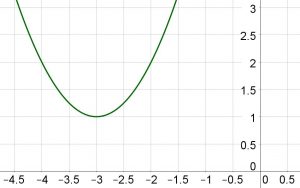
Wir erkennen bereits in der Graphik, dass es keine gemeinsamen Punkte von von $f$ mit der x-Achse gibt. Es kann also keine Lösung geben.
Wie macht sich das in der Rechnung bemerkbar. Wir gehen genauso vor wie im Beispiel vorher:
\begin{align*}x^2+6x+10&= 0 & \color{orange}{\text{Quadratische Ergänzung}} \\\underbrace{x^2+6x\color{orange}{+9}}_{(x+3)^2}\color{orange}{-9}+10&=0 &\text{Binomische Formel} \\(x+3)^2-9+10&=0 & \text{Zusammenfassen} \\(x+3)^2+1&=0 & \big|- 1 \\(x+3)^2 &=-1 & \text{Wurzel ziehen} \\\end{align*}
Die Idee wäre, im nächsten Schritt die Wurzel zu ziehen. Aber: Wir können keine Wurzeln aus negativen Zahlen ziehen. Es gibt keine Zahl, die mit sich selbst multipliziert minus 1 ergibt. Auch algebraisch ergibt sich also: Es gibt keine Lösung.
(An dieser Stelle muss der Hinweis stehen: Die Mathematik löst auch dieses Problem durch eine weitere Festlegung und definiert die sogenannte imaginäre Einheit $i$ als $\sqrt{-1}$. Für weitere Infos verweise ich einfach auf den Wikipedia Eintrag zu Komplexen Zahlen: https://de.wikipedia.org/wiki/Komplexe_Zahl )
x²+8x=-7 – ein weiteres Beispiel zur quadratischen Ergänzung
In den Beispielen vorher haben wir uns langsam rangetastet und wussten aus den vorherigen Beispielen, wie wir vorgehen müssen, um richtig quadratisch zu ergänzen. Doch man hat natürlich nicht immer vorher die passende Hilfsaufgabe.
Wir betrachten mal die linke Seite der Gleichung. Wie müssten wir $x^2+8x$ ergänzen, um mit Hilfe einer binomischen Formel zu vereinfachen? Wir erinnern uns kurz an die binomische Formel \[a^2+2ab+b^2=(a+b)^2 \,.\] In unserem Fall haben wir da bisher stehen \[x^2+8x \,.\] Wir vergleichen die beiden Ausdrücke: Offenbar ist das $a$ in der binomischen Formel bei uns das $x$. Aber das $b$ kann nicht $8$ sein, weil ja in der binomischen Formel noch der Faktor 2 auftaucht. Das $b$ ist also $4$, die Hälfte von 8. Damit ist auch klar, womit wir ergänzen müssen, nämlich mit $b^2$, also mit $(\frac{8}{2})^2=4^2=16$.
Haben wir einen Ausdruck der Form $x^2+px$, so können wir quadratisch ergänzen, indem wir $+(\frac{p}{2})^2-(\frac{p}{2})^2$ ergänzen.
\begin{align*}x^2+8x&= -7 & \color{orange}{\text{Quadratische Ergänzung}} \\\underbrace{x^2+8x \color{orange}{ +\left(\frac{8}{2}\right)^2}}_{(x+4)^2}\color{orange}{-\left(\frac{8}{2}\right)^2}&=-7 &\text{Binomische Formel} \\(x+4)^2-16&=-7 & \big|+ 16 \\(x+4)^2 &=9 & \text{Wurzel ziehen} \\x+4 &= \pm 3 & \big|-4 \\x=-1 \text{ oder } x&=-7\end{align*}
Die Lösungen der Gleichung sind also $x=-1$ oder $x=-7$
Die pq-Formel – Herleitung
Auch Jahre nach Ende der Schulzeit erinnern sich viele zumindestens noch an den Namen pq-Formel. Im Grunde ist die pq-Formel nichts anderes als das Ergebnis einer allgemeinen Durchführung der quadratischen Ergänzung. Der Name pq-Formel kommt dabei daher einfach von den Namen, den man den Variablen gegeben hat. Man kann alle quadratischen Gleichungen durch Umformungen auf die Darstellungsform \[x^2+px+q=0\] bringen.
Löst man eben diese Gleichung ganz allgemein mit den Mitteln, die wir schon kennen, erhält man als Ergebnis die pq-Formel. Wir haben bereits festgehalten, dass wir mit $+(\frac{p}{2})^2-(\frac{p}{2})^2$ quadratisch ergänzen müssen, um anschließend eine binomische Formel zur Vereinfachung zu nutzen.
Los geht’s:
\begin{align*}x^2+px+q&= 0 & \text{Quadratische Ergaenzung} \\\underbrace{x^2+px+(\frac{p}{2})^2}_{(x+\frac{p}{2})^2}-(\frac{p}{2})^2+q&=0 &\text{Binomische Formel} \\(x+\frac{p}{2})^2-(\frac{p}{2})^2+q&=0 & \big|+(\frac{p}{2})^2-q \\(x+\frac{p}{2})^2 &= (\frac{p}{2})^2-q & \text{Wurzel ziehen} \\x+\frac{p}{2} &= \pm \sqrt{(\frac{p}{2})^2-q} & \big|-\frac{p}{2} \\x_{1, 2}&=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q}\end{align*}
Und damit haben wir die pq-Formel hergeleitet:
Eine Gleichung der Form $x^2+px+q=0$ hat die Lösungen \[x_{1,2}=-\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2-q}\]
Längst Kultstatus erreicht hat der p-q-Formel-Song:
Anwendung der pq-Formel – Beispiele
Ich möchte an dieser Stelle gerne 2 Beispiele zur Anwendung der pq-Formel geben. Im ersten Beispiel möchte ich die Gleichung $x^2+8x=-7$, die wir bereits mit der quadratischen Ergänzung gelöst haben, mit der pq-Formel lösen. Wir wissen also bereits, dass die Lösungen der Gleichungen $x=-1$ oder $x=-7$ und haben damit auch direkt eine Kontrollmöglichkeit.
Beispiel 1: x²+8x=-7
Im Grunde muss man sich bei der Anwendung der pq-Formel nur überlegen, was genau denn $p$ und $q$ bei der Gleichung sind. Das ist in der Form, in der wir die Gleichung serviert bekommen nur indirekt möglich. Daher bringen wir die Gleichung zunächst auf die Form $x^2+px+q=0$:
\begin{align*} x^2+8x&=-7 & \big|+7 \\x^2+8x+7&=0 \end{align*}
Wir können also ablesen $p=8$ und $q=7$. Das setzen wir in die pq-Formel ein:
\begin{align*} x_{1, 2}&=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} \\x_{1, 2}&=-\frac{8}{2}\pm \sqrt{(\frac{8}{2})^2-7} \\x_{1, 2}&=-4\pm \sqrt{16-7} \\x_{1, 2}&=-4\pm \sqrt{9} \\x_1=-1 \text{ oder } x_2 &=-7 \end{align*}
Damit sind wir also mit pq-Formel und mit Hilfe der quadratischen Ergänzung – ein gutes Indiz dafür, dass uns keine Fehler unterlaufen sind.
Beispiel 2: 4x^2-24x=32
Quadratische Gleichungen tun uns leider nicht immer den Gefallen und kommen in der praktischen Darstellungsform $x^2+px+q=0$ daher. Insbesondere in der Physik von Wurfbewegungen, die den Schülern auch noch innerhalb der Schullaufbahn begegnet, ist der Faktor vor dem $x^2$ selten 1.
In unserem Beispiel $4x^2-24x=32$ müssen wir auch wieder zunächst ein paar Umformungsschritt tun, um die Gleichung auf die Form $x^2+px+q=0$ zu bringen:
\begin{align*} 4x^2-24x&=32 &\big|-32 \\ 4x^2-24x-32&=0 &\big|:4 \\x^2-6x-8&=0 \end{align*}
Erst jetzt dürfen wir $p$ und $q$ ablesen, es ist $p=-6$ und $q=-8$. Beim Anwenden der pq-Formel muss man jetzt umsichtig mit den Vorzeichen umgehen:
\begin{align*} x_{1, 2}&=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} \\x_{1, 2}&=-\frac{-6}{2}\pm \sqrt{(\frac{-6}{2})^2-(-8)} \\x_{1, 2}&=3\pm \sqrt{9+8} \\x_{1, 2}&=3\pm \sqrt{17} \\x_1=3+\sqrt{17} \text{ oder } x_2 &=3-\sqrt{17} \\ x_1\approx 7,123 \text{ oder } x_2 &=-1,123\end{align*}
Dieses Beispiel zeigt damit zeitgleich, dass die Lösungen quadratischer Gleichungen natürlich nicht immer „glatt“ rauskommen, sondern eben auch irrational sein können.

Die Mitternachtsformel – Für Profis
Wir haben gesehen, dass sich mit Hilfe der pq-Formel alle Sorten quadratischer Gleichungen lösen lassen, wenn wir die Gleichung zunächst durch Umformungen auf die Form $x^2+px+q=0$ bringen.
Die Mitternachtsformel liefert eine Formel, auch die Lösungen einer quadratische Gleichung der Form $ax^2+bx+c=0$ direkt anzugeben – aus diesem Grund wird die Formel auch als abc-Formel bezeichnet. Um die Mitternachtsformel zu erhalten, lösen wir genau diese Gleichung, so wie wir es mit unseren bisherigen Mitteln machen würden. Als erstes stört das $a$ vor dem $x^2$, das werden wir durch die Umformung $:a$ los. Teilt man durch eine Variable, sollte man dies immer hinterfragen: Diese Umformung ist jedoch unproblematisch; Wäre a null, hätten wir überhaupt gar keine quadratische Gleichung. Wir können also beruhigt davon ausgehen, dass $a\neq0$ und dürfen daher auch durch $a$ teilen. Wir formen um:
\begin{align*} ax^2+bx+c&=0 & \big|:a \\ x^2+\frac{b}{a}x+\frac{c}{a} &= 0\end{align*}
Jetzt haben wir die Gleichung auf die Form $x^2+px+q=0$ gebracht und können daher die pq-Formel mit $p=\frac{b}{a}$ und $q=\frac{c}{a}$ anwenden.
\begin{align*} x_{1, 2}&=-\frac{p}{2}\pm \sqrt{(\frac{p}{2})^2-q} \\x_{1, 2}&=-\frac{\frac{b}{a}}{2}\pm \sqrt{(\frac{\frac{b}{a}}{2})^2-\frac{c}{a}} \\x_{1, 2}&= -\frac{b}{2a} \pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}\end{align*}
Dies ist im Grunde eine Version der Mitternachtsformel. Es ist jedoch eine Version, die in den wenigsten Büchern zu finden ist. Der Grund ist simpel: Der Ausdruck lässt sich mit der Kenntnis über Wurzelgesetze noch weiter vereinfachen. Auch optisch fällt schon auf: In jedem Teilausdruck tauch ein $a$ im Nenner auf; das muss also doch auch einfacher gehen. Die Idee ist die folgende: Es ist $\sqrt{\frac{1}{4a^2}}= \frac{1}{2a}$ – das lässt sich nutzen, um den Ausdruck oben zu vereinfachen. Wir klammern dazu unter der Wurzel genau das aus:
\begin{align*} x_{1, 2}&= -\frac{b}{2a} \pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}} \\x_{1, 2}&= -\frac{b}{2a} \pm \sqrt{\frac{1}{4a^2}\cdot\left(b^2-4ac\right)} \\x_{1, 2}&= -\frac{b}{2a} \pm \frac{1}{2a}\cdot \sqrt{b^2-4ac} \\x_{1, 2}&= -\frac{b\pm \sqrt{b^2-4ac}}{2a} \end{align*}
Und das ist auch die Variante, die in den verschiedenen Büchern zu finden ist.
Die Mitternachtsformel hat übrigens ihren Namen daher, dass man als Schüler diese Formel auch beherrschen sollte, wenn man um Mitternacht aus dem Schlaf gerissen wird.
Meine Meinung dazu: Das ist unsinnig. Die Mitternachtsformel bietet keinen Mehrwert gegenüber der pq-Formel oder der quadratischen Ergänzung, sondern ist lediglich eine weitere Option zum Lösen quadratischer Gleichungen.
Ausblick
Wir haben nun erörtert, wie man quadratische Gleichungen auf verschiedene Arten löst und konnten dabei mit der pq-Formel bzw. der Mitternachtsformel sogar eine Lösungsformel angeben.
Man kann sich die Frage stellen, ob es immer möglich ist, eine solche Lösungsformel anzugeben. Wie sieht es bei Gleichungen dritten Grades – das heißt die höchste vorkommende Potenz ist $x^3$ aus? Wie bei Polynomen vierten, fünften und sechsten Grades? Ist es immer möglich, eine solche Formel anzugeben?
Die Antwort lautet: Für Gleichungen dritten und vierten Grades gibt es solche Lösungsformeln: Die Formeln von Cardano, auch Cardanische Formeln. Allerdings sind diese Formeln derartig aufwendig und kompliziert, dass sie fern von jeder Schulmathematik sind. Die Körper- und Galoistheorie liefert dann sogar den Beweis dafür, dass es derartige Lösungsformeln für Gleichungen noch höheren Grades gar nicht geben kann!
In der Schulmathematik beschränkt man sich beim Lösen Gleichungen höheren Grades auf die Nutzung des Taschenrechners, bestenfalls werden Näherungsverfahren, wie das Newton-Verfahren erläutert.
