Baumdiagramm und Vierfeldertafel sind zwei Möglichkeiten zur übersichtlichen Darstellung von Informationen, die zu zwei verschiedenen Merkmalen gehören. In der Schulmathematik ist es häufig Aufgabe, diese Darstellungen zu erzeugen, zwischen ihnen zu wechseln oder mit deren Hilfe statistische Aussagen zu treffen.
Wir widmen uns dem wohl bekanntesten Beispiel zur Bestimmung einer bedingten Wahrscheinlichkeit mit Hilfe einer Vierfeldertafel.
Beispiel: Der Medizintest
Häufig wird als Beispiel der HI-Virus, der zur Autoimmunerkrankung AIDS führt, gewählt. Im Beispiel betrachten wir einen Medizintest für einen fiktiven Virus.
Die beiden zu unterscheidenden Merkmale sind hierbei erkrankt oder nicht erkrankt sowie positiv getestet oder negativ getestet. Sprachliche Verwirrung erzeugt dabei häufig die zweite Merkmalsunterscheidung: Ein positiver Test bedeutet, dass der Medizintest aussagt, dass man an der Krankheit leidet bzw. den Virus in sich trägt.
Von einer fiktiven Krankheit betroffen sind etwa 0,5% der Bevölkerung. Ein Test zeigt bei 98% der Erkrankten tatsächlich ein positives Ergebnis. Allerdings zeigt der Test fälschlicherweise auch bei 1% der nicht Erkrankten Personen ein positives Ergebnis. Wie groß ist die Wahrscheinlichkeit, dass eine Person, die positiv getestet wird, tatsächlich erkrankt ist?
Diesen Infotext können wir mathematisieren zu :
\begin{align*}P(\text{erkrankt})&=0,5% \\P(\text{Test positiv}| \text{erkrankt})&=98%\\P(\text{Test positiv}|\text{nicht erkrankt})&=1%\end{align*}
Erstellen der Vierfeldertafel
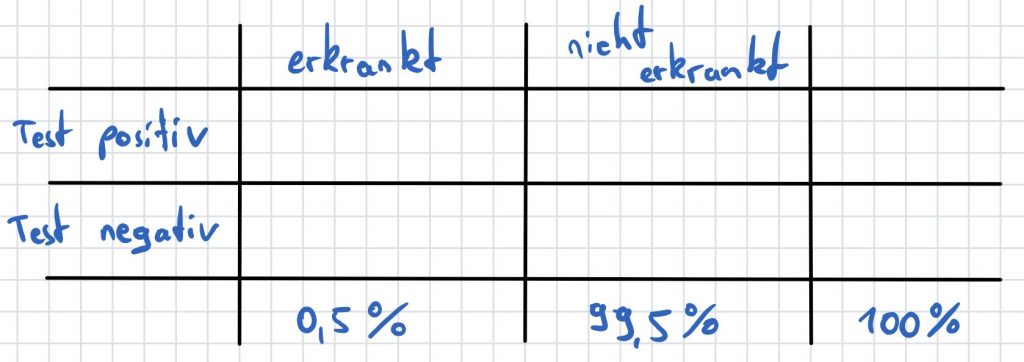
Die Informationen des Fließtextes können wir nun in die Vierfeldertafel übertragen und anhand derer dann die gesuchte Wahrscheinlichkeit bestimmen
Schritt für Schritt:
1. Wir wissen, dass 0,5% der Bevölkerung erkrankt sind. Die übrigen 99,5% sind folglich nicht erkrankt.
2. Von den 0,5% werden 98% positiv getestet, das sind 0,49%.

3. Von den 99,5% der nicht Erkrankten wird 1% fälschlicherweise positiv getestet.
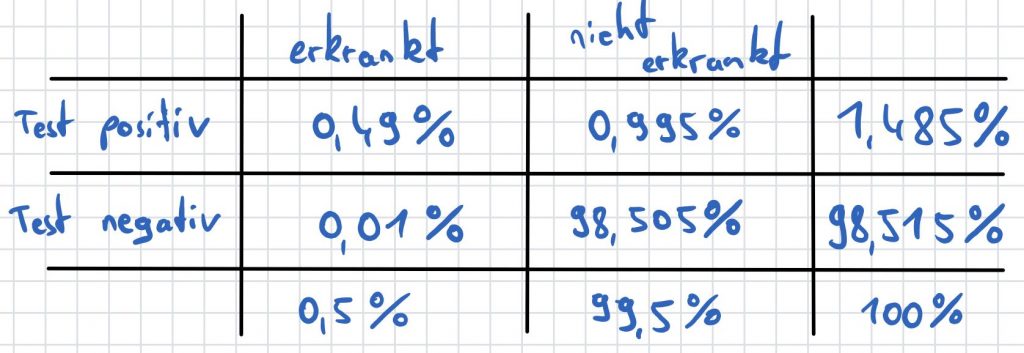
4. Vervollständigung der Vierfeldertafel.5. Gesucht ist die Wahrscheinlichkeit dafür, dass eine positiv getestete Person tatsächlich an der Krankheit erkrankt ist. Wir setzen also bei der bedingten Wahrscheinlichkeit voraus, dass die Bedingung „der Test ist positiv“ bereits erfüllt ist. Wir müssen also in der Vierfeldertafel nur noch diese Zeile betrachten:

Damit ergibt sich folgende Wahrscheinlichkeit
\[P(\text{erkrankt}|\text{Test Positiv}) = \frac{0,49%}{1,485%}\approx 0,33= 33%\]
Eine positive getestete Person ist also nur mit einer Wahrscheinlichkeit von etwa $33%$ tatsächlich an diesem Virus erkrankt. Dieses Wahrscheinlichkeit widerspricht im ersten Moment der Intuition, ist aber Realität. Tatsächliche Tests in der Realitität liegen noch deutlich unter diesem Wert.
Beispielsweise liegt die Wahrscheinlichkeit, nach einem positiven Test auf Scharlach tatsächlich an Scharlach erkrankt zu sein, sogar bei unter 10%.

