Aus dem Zweidimensionalen kennen wir bereits, dass zwei Geraden entweder parallel zueinander sind oder sich in einem Punkt schneiden. Zudem gibt es noch den Fall, dass es zwei Darstellungen derselben Geraden gibt. Man sagt, die beiden Geradendarstellungen sind identisch.
Betrachtet man nun Geraden im Raum, kommt eine weitere Lagebeziehung hinzu. In der Ebene war die einzige Möglichkeit, dass zwei Geraden sich nicht schneiden, dass diese parallel verlaufen. Im Raum gibt es zudem die Möglichkeit windschiefer Geraden.
Inhaltsverzeichnis
Zur rechnerischen Bestimmung der Lagebeziehung von Geraden
Die rechnerische Bestimmung der Lagebeziehung zweier Geraden $g_1$ und $g_2$ verläuft im Allgemeinen in zwei Schritten. In manchen Fällen ist der zweite Schritt nicht mehr nötig.
1.Gibt es gemeinsame Punkte der Geraden $g_1$ und $g_2$?
2. Sind die Richtungsvektoren der Geraden Vielfache voneinander?
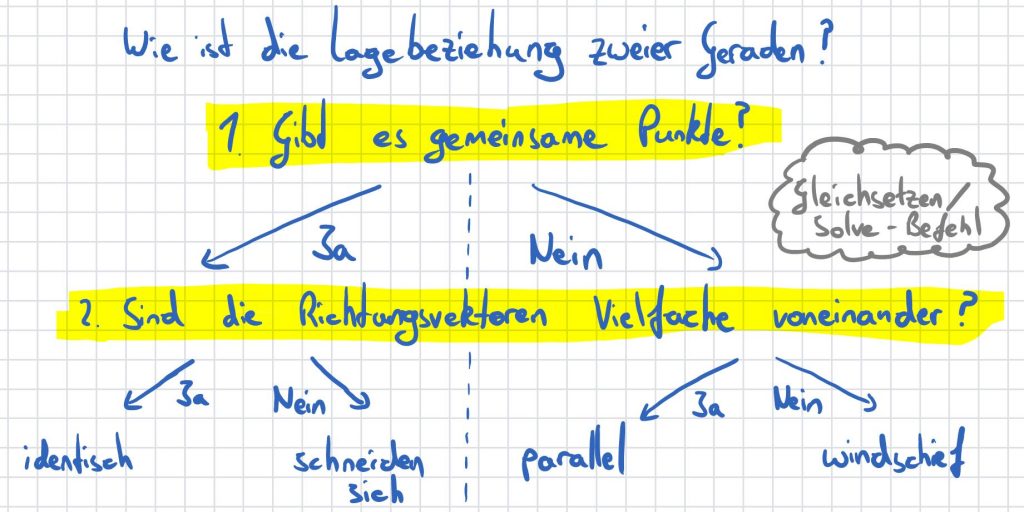
Es folgt je ein Beispiel für die rechnerische Bestimmung mit Hilfe des CAS zu den vier möglichen Lagebeziehungen. Dabei sollte man für $g_1$ und $g_2$ verschiedene Parameter verwenden.
Die Geraden sind parallel

1. Bei der Punktprobe mit Hilfe des solve-Befehls ergibt sich false. Es gibt also keine gemeinsamen Punkte. $g_1$ und $g_2$ können also noch windschief oder parallel zueinander sein.
2. Die Richtungsvektoren sind Vielfache voneinander, der RV von $g_2$ ist das $1,5$-fache des RV von $g_1$. $g_1$ und $g_2$ sind also parallel zueinander.
Die Geraden sind windschief

1. Bei der Punktprobe mit Hilfe des solve Befehls ergibt sich false. Es gibt also keine gemeinsamen Punkte. $g_1$ und $g_2$ können also noch windschief oder parallel zueinander sein.
2. Die Richtungsvektoren sind offensichtlich keine Vielfache voneinander, vgl. $z$-Koordinate. $g_1$ und $g_2$ sind also windschief.
Die Geraden schneiden sich

1. Bei der Punktprobe mit Hilfe des solve Befehls ergibt sich $r=2$ und $s=3$. Es gibt also genau einen gemeinsamen Punkt der beiden Geraden, die Geraden schneiden sich in einem Punkt. Ich erhalte den Ortsvektor des Schnittpunkts der Geraden, indem ich entweder $g_1(2)$ oder $g_2(3)$ bestimme.
2. Überprüfung nicht nötig. Die RV sind keine Vielfachen voneinander. Die beiden ersten Koordinaten des RV von $g_2$ sind identisch, beim RV von $g_1$ jedoch nicht.
Die Geraden sind identisch

1. Bei der Punktprobe mit Hilfe des solve Befehls ergibt sich $r=1,5\cdot s-2$. Dieses Ergebnis mutet zunächst komisch an. Es bedeutet, dass es unendlich viele Lösungen der Gleichung $g_1(r)=g_2(s)$ gibt, es muss lediglich $r=1,5\cdot s-2$ erfüllt sein. Die beiden Geraden haben also unendlich viele gemeinsame Punkte, es müssen daher Darstellungen derselben Gerade sein. Die Geraden sind identisch.
2. Überprüfung nicht nötig. Die RV sind Vielfache voneinander. Der RV von $g_2$ ist das $1,5$-fache des RV von $g_1$.
Zusammenfassung
Eine übersichtliche Zusammenfassung der Bestimmung der Lagebeziehung von Geraden mit dem CAS findet sich in der folgenden PDF:
