Möchte man eine Parameterdarstellung einer Ebene aufstellen, so benötigt man einen Stützvektor und zwei Richtungsvektoren. Oftmals stehen zur Beschreibung allerdings andere Angaben zur Verfügung.
Man muss dann versuchen aus den zur Verfügung stehenden Informationen die benötigten Informationen herausziehen.
Es gibt vier Möglichkeiten zur eindeutigen Bestimmung von Ebenen.
Inhaltsverzeichnis
Ebene aus drei Punkten
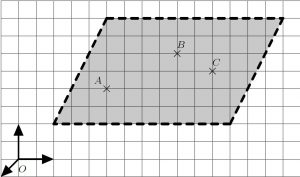
Gegeben sind die Punkte $A$, $B$ und $C$, die nicht auf einer Geraden liegen.
Wähle den Ortsvektor eines Punktes als Stützvektor und die Verbindungsvektoren zu den anderen Punkten als Richtungsvektoren, z.B.
\[E:\vec{x}=\overrightarrow{OA}+r\cdot\overrightarrow{AB} + s\cdot\overrightarrow{AC} \text{ mit } r,s \in\mathbb{R} \]
Ebene aus einer Geraden und einem Punkt
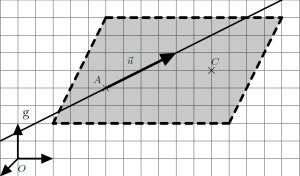
Gegeben sind die Gerade $g$ und ein Punkt $C$, der nicht auf der Geraden liegt. \newline
Erweitere die Parameterdarstellung der Geraden $g$ um einen weiteren Richtungsvektor, beispielsweise die Verbindung des Stützvektors zum Ortsvektor des gegebenen Punktes.
\[E:\vec{x}=\overrightarrow{OA}+r\cdot\vec{u} + s\cdot\overrightarrow{AC} \text{ mit } r,s\in\mathbb{R} \]
Ebene aus zwei parallelen Geraden
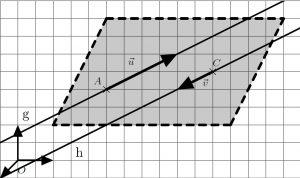
Gegeben sind zwei parallele Geraden $g$ und $h$.\newline
Erweitere die Parameterdarstellung einer Geraden um einen weiteren Richtungsvektor, beispielsweise die Verbindung des Stützvektors zum Stützvektor der anderen Geraden.
\[E:\vec{x}=\overrightarrow{OC}+r\cdot\vec{v} + s\cdot\overrightarrow{CA} \text{ mit } r,s\in\mathbb{R} \]
Ebene aus zwei sich schneidenden Geraden
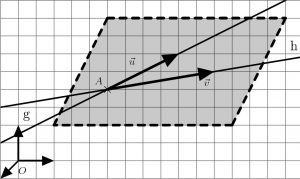
Gegeben sind zwei sich schneidende Geraden $g$ und $h$. \newline
Erweitere die Parameterdarstellung einer Geraden um den Richtungsvektor der anderen Geraden.
\[E:\vec{x}=\overrightarrow{OA}+r\cdot\vec{u} + s\cdot\vec{v} \text{ mit } r,s\in\mathbb{R} \]