Wir kennen bereits die Parameterdarstellung von Geraden: Ausgehend von einem Aufpunkt, der durch den Stützvektor beschrieben wird, durften wir uns beliebig entlang eines Richtungsvektors bewegen. Bei den Ebenen wird nun eine weitere Bewegungsrichtung erlaubt; wir dürfen uns nun also beliebig in zwei verschiedene Richtungen bewegen.
Ein Beispiel für eine Parameterdarstellung einer Ebene E ist:
\[E:\vec{x}=\begin{pmatrix} 2 \\ 2 \\ 9\end{pmatrix} + r\cdot \begin{pmatrix} 1 \\ 8 \\ -1 \end{pmatrix} + s\cdot \begin{pmatrix} 5 \\ 5 \\ 1 \end{pmatrix} \, r, s \in\mathbb{R} \]
Wie schon bei der Parameterdarstellung einer Geraden gibt es auch für die Parameterdarstellung einer Ebene unendlich viele verschiedene Möglichkeiten. Der Stützvektor muss lediglich der Ortsvektor eines Punktes der Ebene sein und die beiden Richtungsvektoren müssen ebenfalls in der Ebene liegen und dürfen zudem keine Vielfache voneinander sein.
Zum Umgang mit Parameterdarstellungen von Ebenen im CAS
Die fundamentale neue Idede bei der Beschreibung von Ebenen ist, dass im Gegensatz zu Geraden, nun zwei Bewegungsrichtungen erlaubt sind. Deswegen benötigt man nun auch zwei verschiedene Parameter und dies muss dem CAS auch mitgeteilt werden. Das erreicht man, in dem man die Funktion abspeichert als $E(r,s)$. Die Darstellung eines Punktes auf der Ebene E mit der Parameterdarstellung ist also abhängig von r und von s.
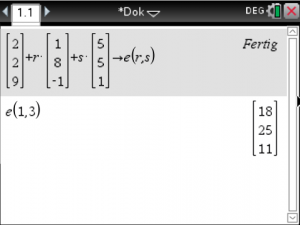
Eine Parameterdarstellung der Ebene benötigt immer zwei Parameter. Deswegen ist eine Beschreibung mit Hilfe von zwei Argumenten nötig. Daher speichert man eine Ebene zum Beispiel als e(r, s) ab. Für beide Parameter dürfen beliebig Zahlen eingesetzt werden und man erhält immer den Ortsvektor eines Punktes der Ebene.
Punktprobe

Die Punktprobe funktioniert bei Ebenen im Prinzip genauso wie bei Geraden mit Hilfe des solve Befehls. Wenn sich bei der Punktprobe mit Hilfe des solve Befehls false ergibt, dann liegt der Punkt nicht in der Ebene.
Wenn sich bei der Punktprobe mit Hilfe des solve Befehls eine Lösung ergibt, dann liegt der Punkt in der Ebene. Im Beipiel ergibt sich $r=1$ und $s=3$. Ich erhalte also den Ortsvektor des Punktes, wenn ich in der Parameter-
darstellung r = 1 und s = 3 einsetze (Vgl. erstes Bild).
