Es ist vielleicht die berümteste Aufgabe, die es im Bereich rund um den Kreisumfang gibt: die Äquatoraufgabe.
Mir sind verschiedene Formulierungen der Aufgabe bekannt. Eine Variante lautet wie folgt:
Ein Seil wird um den Äquator gespannt. Dann wird das Seil um 1m verlängert und so um die Erde gelegt, dass es überall gleich weit von der Erde absteht. Wie weit steht das Seil von der Erde ab?
Nimm dir an dieser Stelle gerne einen Moment, um zu schätzen, wie weit das Seil von der Erde absteht!
Naiv geht man ersteinmal davon aus, dass man für diese Aufgabe Informationen über die Erde wie Erdradius oder Erdumfang braucht. Davon gehen wir auch mal aus, auch wenn wir später in der Profivariante feststellen, dass es auch ohne geht.
Zumindest den Wert für den Erdumfang darf man wissen: Ursprünglich wurde nämlich der Meter so definiert, dass es vom Nordpol bis zum Äquator genau 10 000 km sind. Demnach beträgt der Erdumfang 40 000km.
(Natürlich findet man heutzutage leicht andere Werte als 40 000km; aber die Erde ist ja ohnehin keine perfekte Kugel; die Beschreibung als „Kartoffel“ wäre da deutlich naheliegender.)
Nun kümmern wir uns mal um die Aufgabe:
Es ist immer eine gute Idee, mit Skizzen zu arbeiten. Ich habe die Skizze von oben erweitert: Wir wollen wissen, wie weit das Seil von der Erde absteht. Das habe ich in der Skizze mit dem grünen x veranschaulicht. Außerdem habe ich direkt die Radien eingetragen.
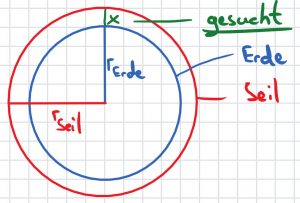
Der Erdumfang ist 40 000km oder eben 40 000 000 m. Folglich ist das Seil 40 000 001 m lang. Wenn wir uns nun überlegen, wie groß die einzelnen Radien sind, wissen wir auch, wie weit das Seil von der Erde absteht.
Es gilt ganz allgemein für den Umfang U eines Kreises mit dem Radius r: $ U= 2\pi r $. Dabei ist $\pi$ die Kreiszahl, es ist $\pi=3,14159….$.
Wir berechnen den Erdradius:
\begin{align*} U_{\text{Erde}} &=2\pi r_{\text{Erde}} \\ 40 000 000m &=2\pi r_{\text{Erde}} \\ r_{\text{Erde}} &\approx 6 366 197,724m \end{align*}
Das geht genauso für den Seilradius:
\begin{align*} U_{\text{Seil}} &=2\pi r_{\text{Seil}} \\ 40 000 001m &=2\pi r_{\text{Seil}} \\ r_{\text{Seil}} &\approx 6 366 197,883m\end{align*}
An dieser Stelle ist es natürlich notwendig, einige Nachkommastellen zu beachten, sonst würde man den Abstand Seil-Erde auf ganze Meter runden.
Es ergibt sich also für den Abstand x von Erde und Seil:
\begin{align*} x&=r_{\text{Seil}} – r_{\text{Erde}} \\ x&= 6 366 197,883m – 6 366 197,724m \\ x&=0,159m \end{align*}
Wenn man man ein Seil um die Erde legt und und es um einen Meter verlängert, dann steht es anschließend überall 15,9cm von der Erde ab!
Das ist ein ganz erstaunlicher Wert und widerspricht in aller Regel der intuitiven Schätzung. Das Ergebnis ist kaum vorstellbar, aber es ist richtig!
Wird um Unterricht der Zusammenhang zwischen Kreisumfang und Radius ermittelt, so wird oft herausgestellt, dass es sich um einen proportionalen Zusammenhang zwischen Umfang und Radius handelt. Das Ausmaß dieser abstrakten Aussage wird erst deutlich, wenn man sich folgendes klarmacht:
Wie groß die Erde ist, ist für die Aufgabe völlig unerheblich! Auch wenn man ein Seil um einen Basketball legen würde und es anschließend um 1m verlängert, steht das Seil vom Basketball 15,9cm ab – genau wie bei der Erdkugel. Dass es sich um einen proportionalen Zusammenhang handelt, heißt eben auch: Verlängere ich den Umfang eines Kreises um 1m, dann ändert sich sein Radius um 15,9cm!
Um diese Einsicht zu stützen, hilft ein Blick auf die Profivariante
Profivariante zur Lösung der Äquatoraufgabe
Man benötigt tatsächlich kein Wissen über den Erdradius oder den Erdumfang. Mit ein wenig mehr Abstraktion kommt man auch ohne diese Werte zum Ergebnis von oben.
Der folgende Ansatz wird auf der Idee beruhen, zwei verschiedene Ausdrücke für $U_{\text{Seil}}$ zu finden.
Relativ einsichtig sind die beiden folgenden Gleichungen:
\begin{align*}U_{\text{Erde}}&=2\pi r_{\text{Erde}} & \text{Das ist gerade die Formel für den Kreisumfang} \\U_{\text{Seil}}&=U_{\text{Erde}}+1m & \text{Das Seil ist genau 1m länger als der Erdumfang}\end{align*}
$U_{\text{Seil}}$ ist aber ja gleichzeitig auch noch gleich $2\pi r_{\text{Seil}}$. Für $r_{\text{Seil}}$ schreiben wir $ r_{\text{Erde}}+x$ und erhalten:
\[U_{\text{Seil}}=2 \pi (r_{\text{Erde}}+x)\]
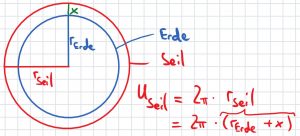
Was jetzt folgt, ist eine Reihe von Termumwandlungen
\begin{align*}U_{\text{Seil}} &= U_{\text{Seil}} \\U_{\text{Erde}}+1m &= 2 \pi (r_{\text{Erde}}+x) \\2 \pi r_{\text{Erde}} +1m &= 2 \pi r_{\text{Erde}}+2\pi x \\1m &= 2\pi x \\x &= \frac{1m}{2\pi} \\x&\approx 0,159m\end{align*}
Im Schritt von der dritten zur vierten Zeile, fällt die Information über $r_{\text{Erde}}$ weg. Das Ergebnis ist also unabhängig von der Größe der Erde.
Die Lösung der Äquatoraufgabe lautet:
Egal, wie groß die Kugel ist: Verlängert man das Seil um 1m, dann steht es anschließend um 15,9cm ab!
